AlphaGeometry : quelles leçons tirer du dernier exploit de DeepMind ?

Consultez la version magazine en cliquant ici

Si vous n’avez qu’une minute à consacrer à la lecture maintenant, voici le contenu essentiel en 7 points) :

1. Deepmind a encore frappé fort avec un système pouvant résoudre des problèmes géométriques de très haut niveau.
2. Ce système propose une combinaison intéressante entre un Large Language Model et un système de validation formelle (appelé ici “IA symbolique”)
3. Le Large Language Model apporte surtout, dans la construction d’une preuve, la capacité à proposer la création de nouveaux éléments (comme la construction d’un point ou une droite)
4. Les systèmes de validation formelle ont pour objectif de combiner les différentes observations pour générer la preuve finale.
5. Un élément fondamental de réussite est la génération de millions de démonstrations exemples synthétiques, sans lequel le modèle n’aurait jamais pu fonctionner.
6. Une première leçon importante porte sur la combinaison entre le LLM et le système de validation qui peut s’étendre à de nombreux autres cas de figure.
7. La seconde importante leçon, que nous connaissions déjà, c’est l’importance vitale d’une donnée synthétique (en notant qu’ici, elle peut être “parfaite”), sans laquelle ce type de résultat ne pourrait même pas exister.

• 5 mots-clés

#IA Symbolique ; #Large Language Models ; #Deepmind ; #Donnée synthétique ; #Exploration de l’espace des solutions

• Pourquoi lire cette publication peut vous être concrètement utile ?

Deepmind a fait beaucoup de bruit avec cette IA pouvant résoudre des problèmes complexes en géométrie. Cette approche nous offre plusieurs enseignements théoriques et pratiques pour adresser d’autres problèmes avec le Deep Learning : comment lutter contre les hallucinations, l’intérêt de la donnée synthétique pour adresser un problème, etc.

• Ce que vous pouvez en dire à un collègue ou à votre boss ?

Datalchemy a détaillé totalement le dernier exploit de Deepmind en IA et en géométrie. En plus, ils s’amusent à en tirer des leçons que nous pouvons appliquer à nos problèmes IA en interne. Déjà sur la data synthétique, mais aussi sur l’utilisation d’un LLM malgré sa capacité à raconter n’importe quoi. Ce qui est amusant, c’est que le LLM n’est qu’une petite partie de la solution, mais cette petite partie est totalement indispensable.

• Quels process métier seront probablement modifiés sur la base de ces recherches ?

La plupart des processus de création confrontés à un simulateur ou un jumeau numérique vont s’inspirer (ou s’inspirent déjà) de ce type d’architecture. Au-delà, les sujets où le problème peut être modélisé d’une manière formelle sont d’excellents candidats pour adapter ces travaux.

• Les cas d’usage que nous avons développé pour des clients qui touchent au sujet de cet écho de la recherche ?

Optimisation d’un jumeau numérique. Contrôle et cadrage d’un Large Language Model.

C’est parti…

Ce mois-ci, nous vous proposons de nous concentrer sur une unique publication, très récente mais qui a eu un impact retentissant dans le monde de l’intelligence artificielle : AlphaGeometry. Ce travail récent de Deepmind a permis de générer un agent pouvant résoudre de nombreux problèmes géométriques issus d’une compétition internationale.

Nous vous proposons de détailler l’approche effectuée par Deepmind, déjà pour rétablir un certain nombre de fantasmes ou contre-vérités qui ont pullulé sur Internet suite à ces travaux. Nous avons par exemple beaucoup entendu parler de l’IA symbolique qui, si elle existe, reste un sujet à préciser. Au-delà, nous allons extraire les éléments les plus importants de l’approche de Deepmind afin d’observer si ce type d’approche peut se généraliser à d’autres sujets. Nous verrons que deux points d’AlphaGeometry peuvent être généralisés et permettent d’envisager une nouvelle forme d’approche en IA qui permette de travailler en utilisant le meilleur des réseaux de neurones, mais en faisant abstraction de leurs plus grands défauts, notamment les hallucinations.

[https://www.nature.com/articles/s41586-023-06747-5]

AlphaGeometry – Analyse en détail d’une IA résolvant des problèmes en géométrie.

Que s’est-il passé ?

Commençons par résumer ce travail et les objectifs qu’il a atteint. Certes, nous faisons usuellement partis des acteurs un peu plus critiques face aux nouveaux travaux en IA, mais nous sommes bien obligés de reconnaître que Deepmind, ici, a obtenu des résultats assez incroyables et particulièrement intéressants.

L’idée fondamentale est d’adresser la résolution d’un problème géométrique euclidien. Le modèle IA (nous restons à haut niveau pour l’instant) va recevoir les bases d’un problème, ici, la présence d’un certain nombre d’éléments géométriques (points, droites, etc.) et de règles sur ces éléments (points alignés, valeurs d’angles etc.). Le modèle IA dispose aussi d’un objectif, une affirmation mathématique qui doit être démontrée rigoureusement à partir des éléments initiaux. Ci-dessous, un exemple de problème soumis au modèle :

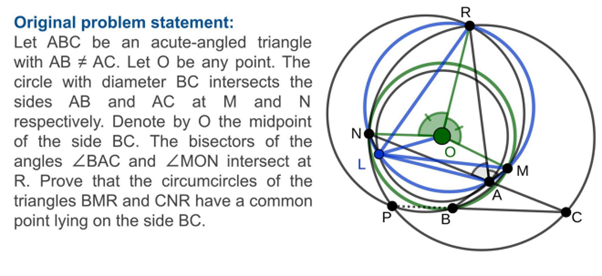
Déjà, concevoir un modèle pouvant résoudre ce type de problème est en soi intéressant. Les mathématiques sont un domaine global qui sous-tend un grand nombre de problèmes logiques plus génériques, et la géométrie est un des domaines des mathématiques assez spécifique : il a d’un côté une “simplicité” de définition appréciable (le nombre d’opérations pouvant être opérées reste limité au regard de ce qu’on peut avoir dans d’autres domaines scientifiques. Mais en même temps, les démonstrations à générer peuvent devenir extrêmement complexes, avec un vrai challenge pour le modèle.

Ici, le coup de canon est venu des résultats du modèle qui a pu résoudre la quasi-totalité des problèmes issus du IMO, international mathematics olympiad, un concours international de très haut niveau.

Autre élément très partagé sur les réseaux sociaux, l’utilisation d’une “IA symbolique”. Les guillemets sont ici indispensables, car si le terme est exact, il a été source de nombreux fantasmes sur les travaux de Deepmind. L’intelligence artificielle peut-elle manipuler des concepts symboliques comme un humain ? La réponse, ici, est non. Et il est temps de creuser ce sujet un peu plus précisément 🙂

IA Symbolique ?

Le terme “intelligence artificielle” est un terme extrêmement dangereux. Ce terme évoque dans l’imaginaire une tonne de fantasmes assez classiques issus de la science fiction, et s’il a été utilisé par les chercheurs en Deep Learning déjà dans les années 1980, il est aujourd’hui source de confusion. Quand on parle de Language Models, d’agents jouant au Go, d’IA Générative, nous parlons en réalité du domaine du Deep Learning, consistant à entraîner des modèles massifs sur une quantité de données qui représente le problème à résoudre. Au-delà d’un simple combat sur les mots, nous avons observé de nombreuses fois qu’il était important d’aller chercher les bonnes définitions, afin de limiter les erreurs de compréhension qui, souvent, nuisent à un projet IA.

Mais alors, qu’est-ce que l’IA symbolique ? Derrière ce terme se cache un gigantesque fourre-tout contenant de nombreuses approches algorithmiques qui était très exploité de 1950 à 1990. On parle d’IA symbolique quand on a un système de règles où on peut construire des solutions par combinaison logique de ces règles. Les systèmes experts, ancêtres du Deep Learning, en font ainsi partie. Dans le cadre d’AlphaGeometry, on parlera d’IA symbolique car on utilisera des moteurs d’inférence mathématiques. Ces moteurs vont stocker un certain nombre de règles afin de construire, à partir d’affirmations sur un problème, de nouvelles affirmations plus complexes. Ces moteurs créent ainsi un graphe en combinant les affirmations stockées et générées, en espérant que le modèle arrive finalement à trouver la preuve que nous cherchons.

Ici, dans AlphaGeometry, deux modèles d’inférence mathématique sont exploités par Deepmind. Il est important de souligner que ces modèles n’ont rien de nouveau par rapport à ce qui existait avant. Ces moteurs sont complétés par un réseau de neurones, un Large Language Model. C’est la combinaison de ces deux outils qui a permis d’obtenir des résultats convaincants par Deepmind, et cette combinaison va particulièrement nous intéresser, en ceci qu’elle a déjà été étendue à d’autres problèmes et présente une solution intéressante à certains défauts du Deep Learning.

Ceci dit, le terme “IA symbolique” doit donc ici être pris avec des pincettes particulièrement fines. Nous n’avons pas de nouvelle forme des outils IA pouvant manipuler des symboles haut niveau. Nous avons des outils relativement anciens qui utilisent un système de règle et de concept pour l’approfondir. Nous verrons plus loin les limites et conditions d’application de ce principe à d’autres problèmes.

Génération de donnes synthétiques

Un point fondamental pour les résultats de Deepmind, et hélas souvent ignoré (car probablement un peu moins sexy que le terme “symbolique”). Hors, ce point est d’une part un élément sans lequel rien n’aurait été possible, et il représente d’autre part une leçon pertinente sur l’intelligence artificielle en général.

En effet, repartons de la base. La révolution de l’intelligence artificielle, débutée en 2012, est basée sur le Machine Learning qui présente un paradigme nouveau. En effet, en Machine Learning, nous n’écrivons plus l’algorithme exact qui va déterminer la solution, nous préférons représenter le problème par un dataset, soit une quantité de données suffisante, pour ensuite générer l’outil par un problème d’optimisation global. L’enjeu est donc d’avoir une donnée suffisamment riche et variée afin de représenter le problème sous l’ensemble de ses facettes. Ce point est souvent bloquant sur un projet IA, où accumuler et annoter une donnée est extrêmement coûteux.

Ici, les auteurs font un choix que nous observons de plus en plus en Deep Learning, depuis le célèbre travail d’OpenAI de Domain Randomization dans lequel les chercheurs entraînaient un agent robotique sur des scénarios totalement synthétiques. Cet axe est un accélérateur de plus en plus utilisé, où on entraîne un modèle sur une donnée synthétique et où on réserve les données réelles à un rôle de test et contrôle de qualité.

Ici, cette approche est fondamentale, et nous proposons de détailler le mode de génération de la donnée synthétique. Deepmind a en effet généré 100 millions d’exemples de démonstrations via une approche très intéressante :

• Dans un premier temps, les auteurs génèrent un grand nombre de figures géométriques plus ou moins complexes. Ces figures sont les points de départ de chaque démonstration.
• Les auteurs vont ensuite utiliser les moteurs “symboliques” mathématiques pour créer de nouvelles affirmations mathématiques, un peu plus complexes. Le moteur peut utiliser ces affirmations comme nouveaux points de départ pour en construire de nouvelles.

Si nous nous arrêtons là, nous aurons généré un exemple de démonstration, mais cet exemple pourra facilement être résolu par le moteur mathématique qui a construit l’arbre d’affirmations. L’originalité est ici de définir des éléments géométriques devant être construits pour arriver à la preuve, autrement dit : les auteurs vont identifier des points, dans le problème généré, qui sont importants pour arriver à la démonstration, mais qui peuvent être omis dans la définition initiale du problème. Ces points deviennent alors des constructions intermédiaires à réaliser pour arriver à la preuve. Et c’est là que nous sortons des résultats que peut générer un moteur symbolique en mathématiques ! Ces moteurs sont en effet incapables de générer de nouveaux éléments géométriques pour ensuite les utiliser dans une démonstration. Le problème devient alors un problème plus complexe qui sera stocké dans le dataset synthétique. Reprenant le schéma de Deepmind :

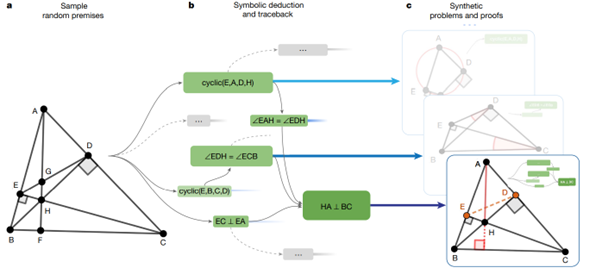
1. Les auteurs partent d’un scénario géométrique initial.
2. Le moteur symbolique construit un certain nombre d’affirmations, jusqu’à conserver une affirmation finale qui sera l’objectif du problème, ci-dessus, le fait que (HA) soit perpendiculaire à (BC). Suite à ce choix, les auteurs suppriment déjà toutes les affirmations générées qui ne sont pas utiles à la solution retenue (dans le schéma, les affirmations conservées sont en vert)
3. Les points E et D ne sont pas utiles à la définition du problème. Ils sont donc considérés comme des constructions intermédiaires que le modèle devra générer, et sont donc enlevés de la définition initiale du problème.

Quand on génère une donnée synthétique, un point important est d’avoir une variance importante dans la donnée. Dit autrement : nous ne voulons pas “juste” plein d’exemples, nous voulons vérifier que cet ensemble d’exemples joue un rôle de représentation valable du problème global à adresser. Ici, les auteurs ont analysé ce dataset, et observé une variance très intéressante : on trouve des problèmes plus petits que gros (schéma ci-dessous), mais avec des cas très différents depuis des problèmes “simplistes’ (colinéarité des points) jusqu’à des problèmes dignes des olympiades, en passant par des théorèmes re-découverts (cas ci-dessous de longueur 20)

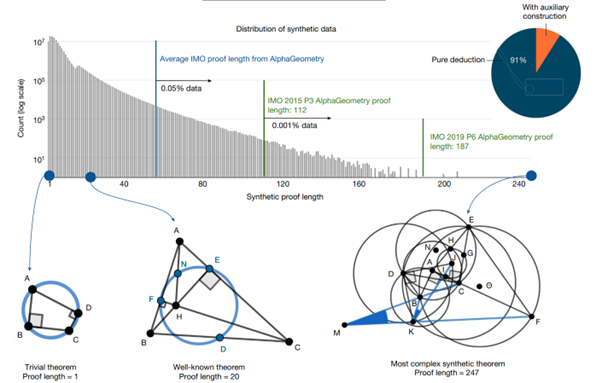
On note que seulement 9% des problèmes générés utilisent des constructions auxiliaires. Ce chiffre peut paraître faible, mais la présence de ces problèmes, nous le verrons, est fondamentale pour la réussite d’AlphaGeometry.

L’alliance du LLM et du moteur symbolique

À ma droite! Un moteur symbolique efficace mais très limité dans ses capacités de recherche, qui a l’avantage de pouvoir explorer un arbre de possibilités d’une manière optimale et de confirmer qu’une solution est valide ou non.

À ma gauche! Un Large Language Model, entraîné à reproduire la distribution d’un langage, capable de résultats époustouflants, mais aussi de ratés prodigieux, notamment d’hallucinations dans ses prédictions qui peuvent se produire à tout moment et sans prévenir.

Personne ne va gagner, et c’est l’alliance de ces deux approches qui permet de générer un outil révolutionnaire de démonstration mathématique. Ce point est d’autant plus intéressant qu’il présage une forme d’utilisation du Deep Learning que nous avons déjà observé et qui permet de s’extraire (dans certains cas) des écueils de l’intelligence artificielle telle que nous la connaissons aujourd’hui.

Commençons par détailler ce qu’a fait Deepmind, avant de s’élever un peu pour réfléchir à la capacité d’adapter ce type de combinaison à d’autres problèmes 🙂

Le Language Model, déjà, est un modèle qui n’est pas si complexe que ça au regard des modèles que nous voyons passer usuellement (GPTs, Llamas, etc), avec environ 100 milliions de paramètres. Ce modèle va être entraîné sur un langage très particulier, modélisant exactement les problèmes géométriques, à compléter des démonstrations. Comme tout modèle Deep Learning, ce modèle est parfaitement capable d’halluciner des absurdités à tout moment, mais est un outil fondamental pour explorer l’univers des possibles et proposer de nouvelles solutions.

Deux moteurs symboliques sont exploités par AlphaGeometry. Ces moteurs vont permettre, à partir d’un ensemble d’observations mathématiques, de rechercher une preuve en appliquant des combinaisons de ces observations qui soient mathématiquement valables.

Le point fascinant est comment ces deux outils sont combinés entre eux. En effet, le Language Model va être utilisé uniquement pour générer des constructions intermédiaires (de nouveaux éléments géométriques) dans le problème. Les moteurs symboliques eux partiront des éléments présents et des constructions ajoutées par le LLM pour essayer de voir s’ils arrivent au résultat par combinaison. En cas d’échec, le LLM sera rappelé avec un prompt enrichi par la dernière expérimentation. Le schéma ci-dessous représente l’approche. Dans le scénario du haut du schéma, le LLM a juste généré le point D milieu de [BC]. D’une manière générale, les apports du LLM sont ci-dessous surlignés en bleu.

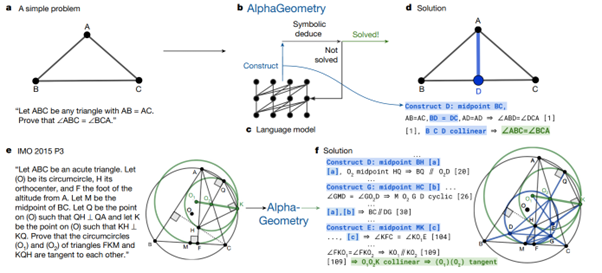
Prenons un peu de hauteur. La combinaison de ces modèles est ici intéressante, nous avons, à haut niveau :

• Un modèle Deep Learning génératif qui va apprendre la distribution de la donnée et générer des nouveaux éléments originaux, avec une capacité de création incontestable. Ce modèle est en revanche capable de raconter n’importe quoi à tout moment (le drame des hallucinations qui dure depuis 2012…)
• Un système qui permet de tester et de valider (ou non) un élément généré. Ce système sert de boussole pour filtrer (voire, diriger) l’utilisation du modèle Deep Learning.

Ce type d’approche n’est pas fondamentalement nouveau, nous avons déjà rencontré des sujets de génération qui l’utilisent directement. Le cas de la robotique avec jumeau numérique n’est typiquement pas très éloigné, où nous allons avoir un agent entraîné via du Deep Reinforcement Learning pour générer de nouvelles actions, mais où ces actions vont être validées contre le jumeau numérique avant d’être conservées et utilisées.

Ce type d’approche risque d’exploser en combinaison avec les modèles de langage comme les GPTs, Mistral ou autre LLamas. En effet, aucune technique ne permet de se prémunir correctement et absolument contre les hallucinations. Dès lors, créer un algorithme qui va régulièrement interroger un de ces modèles pour ensuite confirmer que le résultat est correct, pour, si le résultat pose problème, ré-interroger le modèle, est une approche beaucoup plus constructive et fiable que ce qui existe dans la majorité des cas. Et nous avions d’ailleurs repéré un de ces cas dans une de nos revue de recherche, parue en juin 2023 (https://datalchemy.net/ia-quel-risque-a-evaluer-les-risques/). En effet, des chercheurs avaient développé un agent jouant à Minecraft qui opérait ce type d’itérations, entre suggestions d’un modèle de langage et validation formelle.

Cette alliance est peut être une des “gemmes cachées” de la publication, en ceci qu’elle présage une approche très générique pour adresser de nouveaux problèmes. Nous (Datalchemy) avons déjà eu l’occasion d’implémenter ce type d’échange (à un niveau beaucoup plus humble, faut-il le préciser) pour avoir des résultats très intéressants. Ceci-dit, nous voyons déjà que nous sommes sur des implémentations loin d’un traitement temps réel, plus sur des approches d’exploration. Conception/design de nouveaux objets ou mécanismes face à un jumeau numérique, optimisation de problèmes physiques, robotiques sont déjà des évidences. Au-delà, on peut s’intéresser à l’extension à un problème logique qu’illustre ici parfaitement la géométrie. La pertinence d’une telle extension sera directement liée à la capacité que nous aurons à modéliser correctement, via un système de règles, un modèle valable. La géométrie (et les mathématiques plus généralement) sont le cas d’école “le plus simple”, en ceci qu’une démonstration mathématique n’est, par nature, pas confrontée à une expérience réelle. Plus le sujet cible sera aléatoire, relié à des opérateurs humains ou complexe à modéliser “parfaitement”, moins l’approche sera intéressante. Ceci dit, nous pouvons imaginer des approches permettant non pas d’automatiser la découverte de la solution, mais son accélération, en modélisant uniquement pour filtrer le mieux possible les prédictions d’un LLM et pour ne garder que les échantillons les plus intéressants pour consultation d’un expert.