Why you should read this publication

Let’s be honest and warn the reader: two-thirds of this article is more technical than usual. That said, in this article we discuss a fundamental new architecture that could tomorrow revolutionize many Deep Learning approaches, as we move towards a better understanding of generative AIs and, in particular, the diffusion models that have been driving these AIs for some years now. Finally, the universal simulator heralds a new type of tool for working in robotics or, more generally, in image-based gesture representation, which, while it may have a few pitfalls, will revolutionize everyday work in these fields.

What business processes are likely to change as a result of this research?

UniSim can revolutionize robotics and object interaction learning, such as working with human gestures captured on video.

Kolmogorov-Arnold networks are already an interesting candidate for approximating simple phenomena by complex functions.

Finally, a better understanding of diffusion patterns will have a strong impact on all AI image generation tools, beyond the voodoo rituals supposed to give efficient prompts.

If you only have a minute to devote to reading now, here's the essential content in a nutshell

1. Deepmind and Berkeley teamed up to create a “universal” simulator, capable of taking an image and action instructions as input and generating a video simulating the result as output. This work required the accumulation and aggregation of many different and complementary datasets. The authors can control this simulator and have been able to train a robotic agent solely in simulation, and then use it in the real world.
2. And now something completely different: a new fundamental architecture has appeared and is causing quite a stir in the research world, called Kolmogorov-Arnold Networks. These models are still reduced to simple cases, but seem to be very efficient. In the future, they claim to be able to dethrone the MLPs that are everywhere in Deep Learning today.
3. Finally, a new study lifts an exciting veil on the diffusion models that have become the essential architecture for image-generating AIs. Among other discoveries: these models quickly become quite independent of the training dataset, and their architecture is naturally suited to image generation.

A “universal” stock simulator?

Hailed as “outstanding ” at the last ICLR 2024, the article Learning Interactive Real-World Simulators by Yang et al. brings together some very fine minds from Deepmind and Berkeley to produce a rather impressive piece of work.

The question posed here is to push the so-called generative AI models (these diffusion models which, over the past three years, have cordially imposed themselves on the landscape, among others via the famous Stable Diffusion) beyond the simple generation of images or videos. The idea is to use these models to simulate reality by conditioning them on actions. In other words, where today we can generate an “artistic” video via a prompt, is it possible to generate a video based on an initial image (representing a situation) and a series of imaginary actions. At this stage, an illustration would be an effective way of visualizing the challenge:

Above, for each column, the first image is an initial state taken from our good old reality, with a “prompt” above it. The three images below show what the model has generated, a video representing these actions performed visually.

The project is therefore very ambitious: to have a model capable of predicting the evolution of a real system and generating images corresponding to these predictions. And as usual in Deep Learning, the most important thing is the data representing the problem. So it’s no coincidence that this publication opens with the generation of a gigantic dataset, itself derived from many different datasets. Most of these original datasets come from the research world and represent fairly similar problems: executions in synthetic environments, real robotic data, real human activity, and even image/text data from theInternet.

Bringing together such diverse data is obviously no mean feat, if only to define a common final model. Here, the video is preserved as a series of images, and the description texts are transformed into embeddings via a classic T5 model, to which robotic actions are concatenated if present. This space will be the action space of the model, the inputs from which it will generate the prediction. Three interesting details:

• For panorama scans above, the challenge is to simulate the movement of an agent and therefore the evolution of its camera as it moves. The authors start with a static panorama, then generate movements by moving a limited preview of this panorama.
• For synthetic data (one of our main focuses at Datalchemy), the authors insist on its importance, particularly for generating rare cases that are rarely encountered in real data. This approach is now a classic in Deep Learning.
• For images taken fromInternetthey are considered as videos with a single frame. The image annotation is used as an action (for example, a person walking in the street)

At this point, habemum datasetIn this case, we can talk about the model. This will take as input a first image (the initial state) and the description of the action, in order to generate future observations depending on this action. This may be a coded camera movement, the actions of a robot arm or, more simply, natural language. The model (see diagram below) is unsurprisingly a broadcast model, which learns to generate one image after another via a denoising operation (more on this later).

Before embarking on the use of such a model, a reality-check is essential: the authors trained their model on 512 TPU v3 for 20 days. In other words, as a quick approximation, a small budget of €500,000 is required (for a single training) to reproduce this result…

With that in mind, let’s take a look at the results of this model below:

• Top left: the model can simulate the visual result of fairly complex human interaction actions, such as washing or drying one’s hands. Note that an action target (here, the carrot) can be designated freely via natural language, which is one of the strengths of Large Language Models and other cross embeddings
• Top right: interaction with buttons and an electrical system
• Bottom left and right: “navigation” through the simulator, moving from an initial scene.

Keep these examples in mind, as they will serve as a basis for critiquing this work in the remainder of this article.

The fundamental application at present is to use this “universal simulator” to train robotic agents without the need for interactions with reality (often impossible in training), or for a specialized simulator. This is a fascinating application, since it links up with the field of Deep Reinforcement Learning which is not without its pitfalls, especially when it comes to the problem of transferring an agent from a simulated environment to a real one. Difficulties often arise from the visual limitations of the simulated environment, as well as those associated with modeling complex interactions satisfactorily. Here, the authors present an agent trained solely on UniSimwith a more-than-classic algorithm (Reinforce) and to observe its generalization to real cases, as shown in the diagram below:

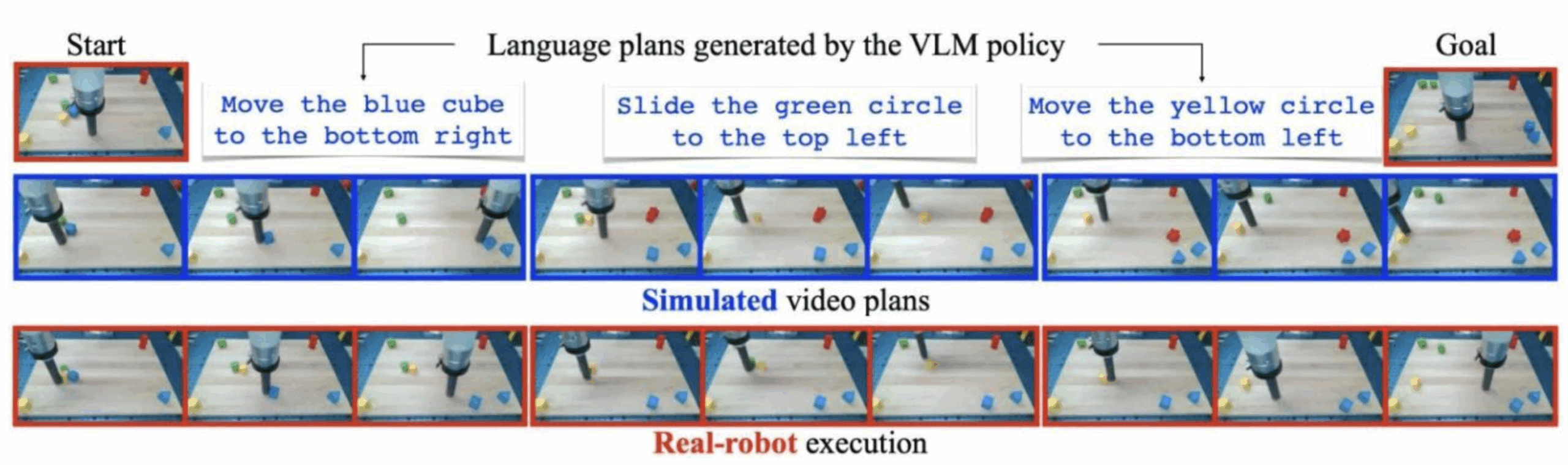
But then, revolution? Maybe yes, maybe no 😊 Our main mission at Datalchemy is to follow the research and filter it ruthlessly to enable our customers to use the latest, most effective approaches. And while we’ve done a lot of work in robotics and Deep Reinforcement Learning (see our previous article onImitation Learning), we can’t imagine using such a tool if it were available. Explanations:

Here, talking about simulator is actually a bit of an exaggeration. In theory, a simulator reproduces a certain number of physical rules (gravity, contact between objects, etc.) to determine the consequences of an action. Unisimlearns from a gigantic dataset predict future images from a history of images and a description of actions. Perhaps it has modeled physical rules in its internal space that it has learned during training, but even if this is the case, these physical rules will not be easy, if not impossible, to extract (see our previous review on the interpretability of the Deep Learning). In addition, a Deep Learning will always be able to make a wrong prediction at any time (hallucinations), and without warning. Here, detecting such an error will be particularly complex, if not impossible. It’s worth noting that for certain problems that were under-represented in the data, the authors observed that it was necessary to prefix the prompt to designate the dataset containing these problems to make it work:

The real question, of course, is one of generalization. The authors’ experience of training an agent on Unisim and then apply it to a real case is very limited (moving very simple geometric shapes) compared to the complex predictions presented in the publication… The authors are quite honest about these limitations in their work. Among other things, they note that it is perfectly possible to give an absurd command and observe the result (ask a robot arm to wash its hands). Among other limitations: a very large model is too memory-intensive and consequently has trouble taking in enough images to model a complex problem. The fact that it only manipulates images makes it “blind” to other action parameters, such as the force exerted on a robot arm.

That said, it remains an interesting piece of work, continuing the natural language approaches to robotic control that Google has regularly offered (the famous RT-1 and RT-2). A subject to keep an eye on!

Kolmogorov-Arnold Networks.

Warning. The content of this paragraph may be a little more technical than usual…

The KANsor Kolmogorov-Arnold Networksare a new fundamental architecture for Deep Learning architecture that has been causing quite a stir in the research world since the release of the eponymous paper by Liu et al.. Please note: we’re not talking about a new approach to creating Large Language Modelsor to control a robotic agent, but a much more fundamental architecture that is destined to replace MLPs (multi-layer perceptrons). The latter are the ancestral architecture of Deep Learningarchitecture, which is irreplaceable, and can be found scattered throughout all existing architectures, up to and including Large Language Modelsin addition to the Transformer. This architecture is regularly put to good use, for example when working with 3-dimensional point clouds, or directly on images with the famous MLPMixer. Tackling this architecture is no innocent matter, and can prove particularly interesting.

Let’s delve into the technical details. The principle here is to start from a fairly fundamental mathematical concept, that of universal approximation. The idea is that, whatever the function we want to approximate, we can do so with an error as low as we like, via a MLP sufficiently complex. This notion of universal approximation is fundamental in the world of Deep Learning. The authors thus propose to draw inspiration from another mathematical approximation theorem, the representation of Kolmogorov-Arnoldto propose a radically new architecture with fascinating results.

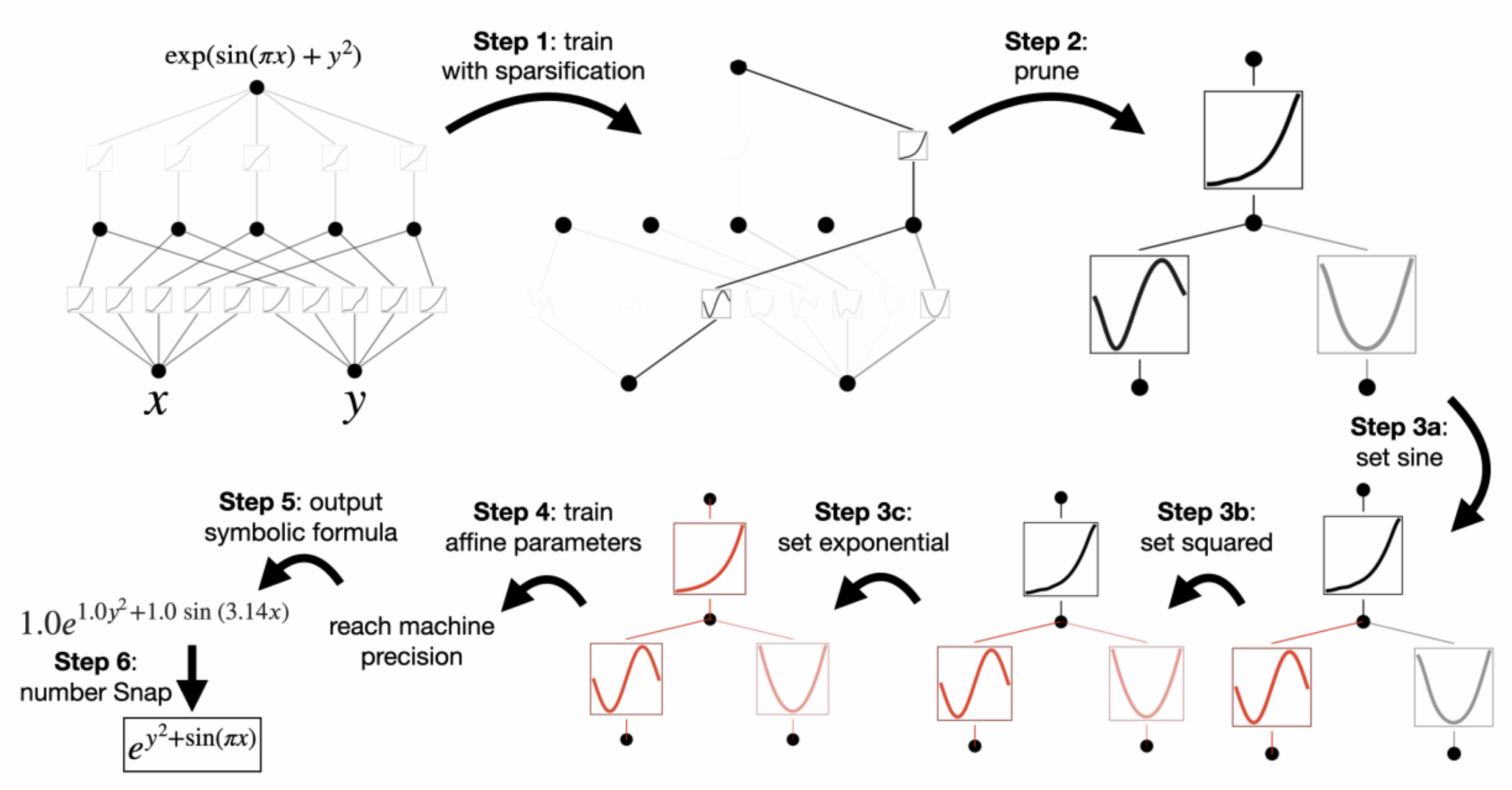
It should be noted that other researchers had tackled the subject, but had stumbled over the fact that to apply this theorem directly was to produce a two-layer neural network, naturally limited in its expressive capacity. The authors therefore worked on extending the initial definition to create networks of variable size, with a dynamic complexity approach enabling the model to adapt during training. But we’re getting ahead of ourselves: what is a KANand how does it differ from MLP ? The diagram below summarizes the key points:

On the left, we find the good old MLP. The activation functions are fixed (usually the classic ReLU) and each node has these parameters available for learning (the weights). Each node expresses a linear combination of input values.

The KAN shown on the right is radically different. The nodes simply add up the values received, with no parameters to be learned. The links between nodes, on the other hand, model combinations of elementary mathematical functions (such as splines), and this combination is subject to learning. Indeed, the Kolmogorov-Arnold states that any multivariate continuous function on N variables can be expressed as the finite composition of a continuous function of a single variable. In other words, the only combination of several variables will be the sum, and the important information will be learned about each variable separately to model the target function.

Note that in the approach presented, the authors propose a way of simplifying a KAN after learning it, in order to obtain the simplest possible network that addresses the problem to be solved. The resulting models are particularly effective, as in the example below where we want to learn how to model a specific mathematical function. Visit pruning removes the unnecessary parts of the network, after which we observe that the network has learned to model each part of the mathematical function until it finds the formula we wanted to learn.

We won’t delve any further into the details, but instead take a step back to question the value of this scientific work. The most beautiful mathematical models won’t impose themselves in our field without specific experimental results. And while these results are indeed interesting, they remain a little limited for us to be able to project ourselves easily.

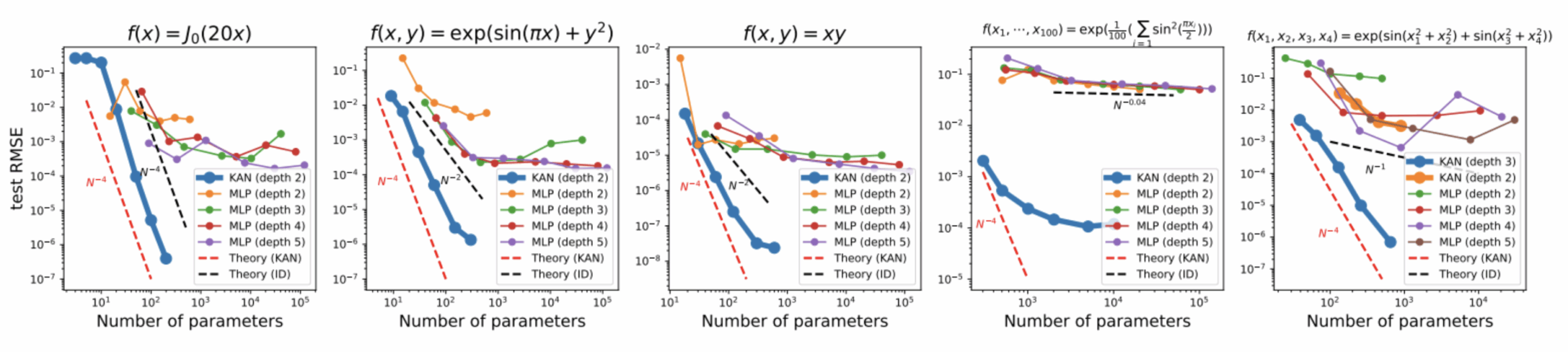
The first result, based on fairly basic synthetic data, is that the authors observe that KANs converge much faster than MLPs with less complexity. Below, we have at the top the target mathematical function we want to reconstitute, and curves showing the error as a function of the complexity (number of parameters) of the network.

The second result (we’ll skip a few) concerns the solution of partial differential equations. The solution of this type of equation is often used in physics to model complex systems, such as strength of materials or fluid dynamics. Here, on a very simple problem, the KAN seems to far outstrip their cousins in terms of results and effectiveness. MLPs.

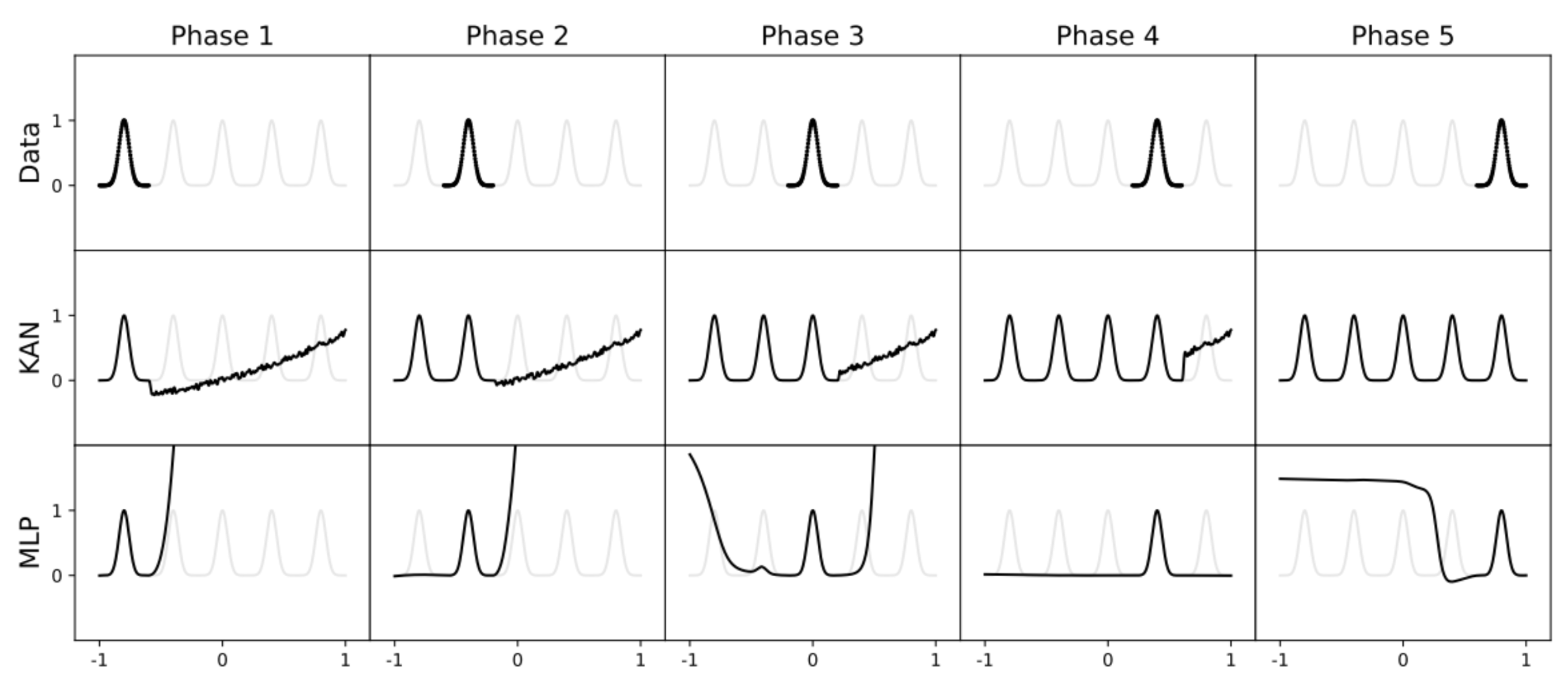
Last but not least, a scenario reproducing a continuous learning approach. Below, the model will receive the data sequentially (with dots from left to right). We can see that the MLP will quickly forget the previously received data, whereas the KAN will continue to learn without destroying the previous information:

Other results are presented, but they all have in common that they take very simple problems, on which the authors observe a superiority of their architecture over the MLP.

But should we react immediately and use these models? Obviously not. It’s urgent to wait and watch academic developments closely over the coming months. Many researchers have already begun testing this architecture on more applied problems. It’s this replication of research that will decide whether this architecture is relevant or not. At the very least, we’d like to point out the efficiency of this approach, and a certain form of mathematical flexibility that will appeal to the enlightened amateur, who will be wary of his own biases and therefore wait for further results.

A better understanding of distribution models and their priors

Another work of great interest to us this month, also honored as outstanding at the last ICLR, Generalization in diffusion models arises from geometry-adaptive harmonic representations by Kadkhodaie et al lifts an interesting veil over the workings of diffusion models.

We talked about it at the start of this review, but let’s put it another way: diffusion models are an architecture that has been in the limelight since 2021, and which has established itself in the field ofAI field, rather violently replacing their predecessors, the Generative Adversarial Networks thanks to a tenfold increase in efficiency. This approach teaches how to iteratively denoise images, thus creating a generation system that takes a “noise image” as input and, through successive calls, generates a high-quality final image as output. Diffusion has established itself in the generation of images, 3D point clouds or video, as well as in other fields such as Deep Reinforcement Learning (via Diffusion Policy discussed in a previous review) or audio generation.

A question that has been agitating the scientific community for some years now is why this denoising approach is so effective compared to other, more intuitive approaches. This is the question the authors set out to answer. Although their work leaves more questions than answers, it nevertheless lays the foundations for a better understanding that will feed future work in the field in an exciting way. The authors also study another phenomenon: the “rote” learning of dataset especially when the latter is small in size…

The authors’ first experiment is fascinating. They train a broadcasting model to generate images with datasets of different sizes: 10 images, 100, 1000, 10,000 and 100,000 images. More precisely, for each size of dataset two different models and compare their results, as shown below:

Above, we have :

Top: 2 models (S1 and S2) were trained on 1,10,…,100,000 images. Each time, the models had datasets totally different training datasets (no shared elements between datasets). It can be seen that for small image volumes (1,10,100), the images generated by the model are exactly those of the datasetsas shown by the images closest to dataset (Closest image from…) recovered each time. On the other hand, and this is what’s most fascinating, considering that it’s the same input noise for each model, we observe that at around 100,000 images, the image generated by S1 is extremely close to that generated by S2! Considering that they have no shared images in their datasetsThis proximity is quite astonishing! We can see that the closest images from the datasets are different from the generated images – we are indeed generalizing.

Bottom: we see the similarity between pairs of images generated by the two models for different volumes of datasets training. We observe that for a dataset of 100,000 images, two images generated by the two models are much closer than images from the dataset.

The conclusion is that models learn to behave very closely where their datasets are disjointed. This is a very surprising point, especially since in Deep Learningwe quickly get into the habit of linking any phenomenon to the dataset training. The explanation proposed by the authors is that diffusion models are structurally able to generalize easily to image generation. We’re talking here about prior structure. The authors note that the treatment of the generation model can be expressed via a rather interesting mathematical basis, named here geometry-adaptive harmonic bases (GAHB). The diagram below shows how an image, noisy plus denoised by the diffusion model, can be expressed in terms of this internal model basis:

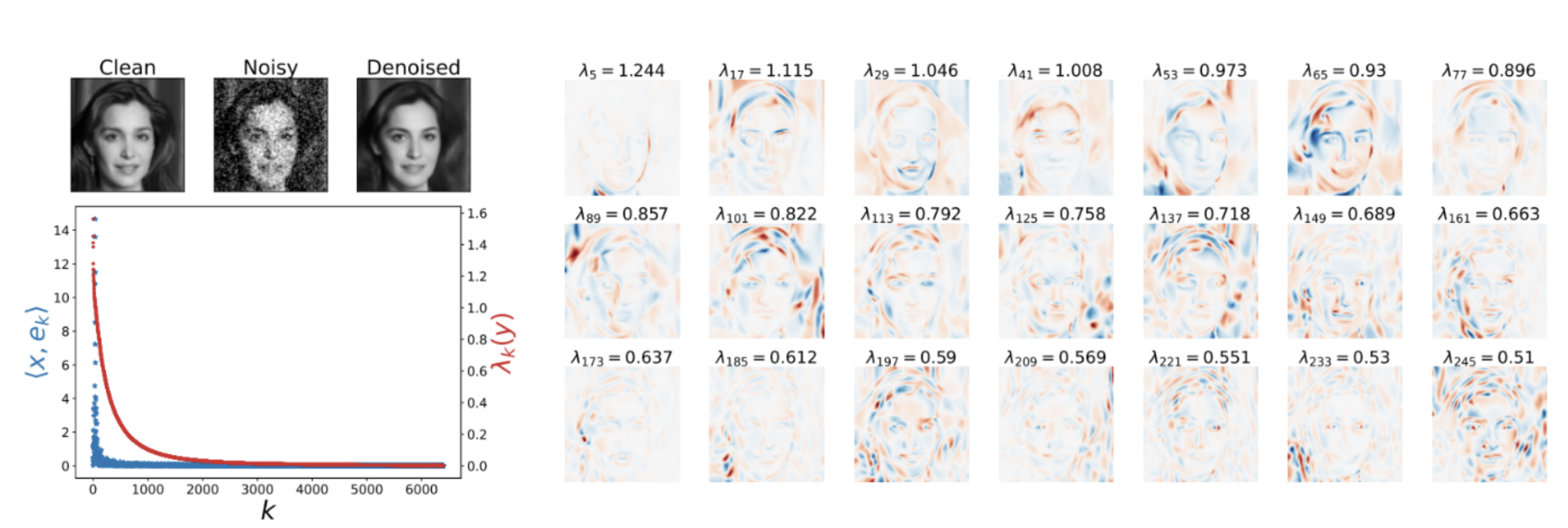
Top left: the initial image, its noisy version and the denoised version from the diffusion model.

Bottom left: the abscissa shows the index of each element in the database, and the ordinate shows the importance given to each element. We can see that a very small number of elements have non-zero values; in other words, the model observes a reduction in the complexity of the image to be denoised by expressing this image over a small number of elements in the database.

Right: the information carried by various base elements. Visually, we can see that the information strongly follows the contours of the image to be denoised, with oscillations between positive (red) and negative (blue) values. This observation is the starting point for more hypothetical analyses. The idea is that a diffusion model will naturally express information according to oscillations on this decomposition basis GAHB. A test on much simpler images also shows these oscillations, and supports the idea that this decomposition is a “natural” function of diffusion models, facilitating their image management:

Both conclusions are particularly captivating. I would, however, confess a preference for the first observation, i.e. the fact that two trained models out of two datasets from the same dataset arrive somewhere at the same result. This strongly supports the idea that diffusion models bring strong structural information to the data to facilitate image learning. Beyond that, the observation of decomposition is interesting, but unfortunately leaves us wanting more. What exactly do these GAHB ? How can this decomposition be used? Once again, we’ll have to wait and see what happens next in this line of research. 😊