Why you should read this publication

Deepmind has caused quite a stir with this AI that can solve complex problems in geometry. This approach offers us a number of theoretical and practical lessons for addressing other problems with Deep Learning: how to combat hallucinations, the value of synthetic data in addressing a problem, and so on.

What you can say to a colleague or your boss?

Datalchemy has fully detailed Deepmind’s latest feat in AI and geometry. What’s more, they have fun drawing lessons from it that we can apply to our in-house AI problems. Already on synthetic data, but also on the use of an LLM despite its ability to talk nonsense. The funny thing is that LLM is only a small part of the solution, but that small part is totally indispensable.

What business processes are likely to change as a result of this research?

Most of the creative processes confronted with a simulator or digital twin will be inspired (or are already inspired) by this type of architecture. Beyond that, subjects where the problem can be modeled in a formal way are excellent candidates for adapting this work.

the use cases we have developed for customers that touch on the subject of this research review

Optimizing a digital twin. Control and framing of a Large Language Model.

If you only have a minute to devote to reading now, here's the essential content in a nutshell

1. Deepmind has struck again with a system capable of solving very high-level geometric problems.
2. This system offers an interesting combination of Large Language Model and a formal validation system (referred to here as “symbolic AI”).
3. The Large Language Model brings above all, in the construction of a proof, the ability to propose the creation of new elements (such as the construction of a point or a line).
4. The aim of formal validation systems is to combine the various observations to generate the final proof.
5. A fundamental element of success is the generation of millions of synthetic example demonstrations, without which the model could never have worked.
6. A first important lesson concerns the combination of the LLM and the validation system, which can be extended to many other scenarios.
7. The second important lesson, which we already know, is the vital importance of synthetic data (noting that here, it can be “perfect”), without which this type of result couldn’t even exist.

Here we go...

This month, we’re focusing on a single, very recent publication that has had a resounding impact on the world of artificial intelligence: AlphaGeometry. This recent work by Deepmind has generated an agent capable of solving numerous geometric problems from an international competition.

We’d like to take a closer look at Deepmind’s approach, to set the record straight on a number of fantasies and untruths that have proliferated on the Internet as a result of this work. For example, we’ve heard a lot about symbolic AI, which, if it exists at all, remains a subject to be clarified. Beyond that, we’re going to extract the most important elements of Deepmind’s approach, to see if this type of approach can be generalized to other subjects. We’ll see that two points from AlphaGeometry can be generalized to allow us to envisage a new form of approach in AI that makes it possible to work using the best of neural networks, but disregarding their greatest shortcomings, notably hallucinations.

[https://www.nature.com/articles/s41586-023-06747-5]

AlphaGeometry - Detailed analysis of an AI solving problems in geometry. What happened?

Let’s start by summarizing this work and the objectives it has achieved. Admittedly, we are usually among those who are a little more critical of new work in AI, but we have to admit that DeepmindHere, we’ve come up with some incredible and particularly interesting results.

The fundamental idea is to address the resolution of a Euclidean geometric problem. The AI model (we’re staying at the high level for now) will receive the basis of a problem, in this case, the presence of a certain number of geometric elements (points, lines, etc.) and rules about these elements (aligned points, angle values, etc.). The AI model also has an objective, a mathematical assertion that must be rigorously demonstrated on the basis of the initial elements. Below is an example of a problem submitted to the model:

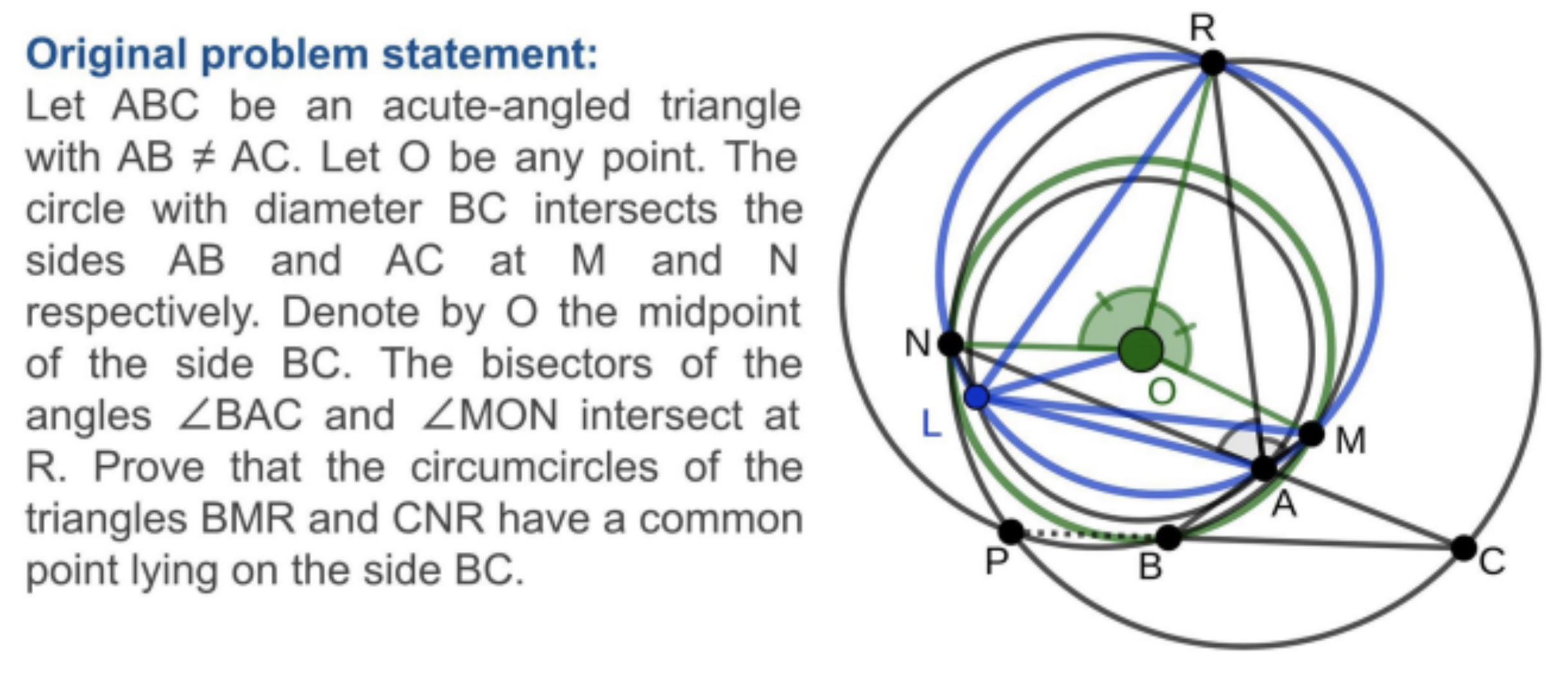
Already, designing a model that can solve this type of problem is interesting in itself. Mathematics is a global field that underlies a large number of more generic logical problems, and geometry is one of the fields of mathematics that is quite specific: on the one hand, it has an appreciable “simplicity” of definition (the number of operations that can be performed remains limited compared to what we can have in other scientific fields. But at the same time, the demonstrations to be generated can become extremely complex, with a real challenge for the model.

Here, the coup de canon came from the results of the model, which was able to solve almost all the problems arising from the IMO, international mathematics olympiada top-level international competition.

The use of “symbolic AI” is another element that has been widely shared on social networks. The quotation marks are essential here, because if the term is accurate, it has been the source of many fantasies about the work of Deepmind. Can artificial intelligence manipulate symbolic concepts like a human? The answer here is no. And it’s time to dig a little deeper into this subject 🙂

Symbolic AI?

Artificial intelligence” is an extremely dangerous term. The term conjures up a ton of classic science fiction fantasies, and although it was used by Deep Learning researchers as far back as the 1980s, it is now a source of confusion. When we talk about Language Models, agents playing Go, Generative AI, we’re really talking about the field of Deep Learning, which consists of training massive models on a quantity of data that represents the problem to be solved. Beyond a simple battle over words, we’ve observed time and again that it’s important to get the definitions right, in order to limit the misunderstandings that often hamper an AI project.

But then, what is symbolic AI? Behind this term lies a gigantic catch-all containing numerous algorithmic approaches that was much exploited from 1950 to 1990. We speak of symbolic AI when we have a system of rules where we can construct solutions by logically combining these rules. Expert systems, the ancestors of Deep Learning, belong to this category. In the case of AlphaGeometry, we speak of symbolic AI because we use mathematical inference engines. These engines will store a certain number of rules in order to construct new, more complex assertions from statements about a problem. These engines then create a graph by combining the stored and generated assertions, in the hope that the model will eventually find the proof we’re looking for.

Here, in AlphaGeometrytwo mathematical inference models are exploited by Deepmind. It’s important to stress that these models are nothing new compared to what existed before. These engines are complemented by a neural network, a Large Language Model. It is the combination of these two tools that has enabled us to achieve convincing results by Deepmindand this combination will be of particular interest to us, in that it has already been extended to other problems and presents an interesting solution to some of the shortcomings of Deep Learning.

That said, the term “symbolic AI” should be taken with particularly fine-toothed brushes. We don’t have a new form of AI tool that can manipulate high-level symbols. We have relatively old tools that use a system of rules and concepts to deepen it. We’ll see later on the limits and conditions of application of this principle to other problems.

Synthetic data generation

This is fundamental to the results of Deepmindand unfortunately often ignored (as it’s probably a little less sexy than the term “symbolic”). However, on the one hand, this is an element without which nothing would have been possible, and on the other, it represents a pertinent lesson about artificial intelligence in general.

Indeed, let’s start from the very beginning. The artificial intelligence revolution, which began in 2012, is based on the Machine Learning which presents a new paradigm. Indeed, in Machine Learningwe no longer write the exact algorithm that will determine the solution, preferring to represent the problem as a datasetIn other words, a sufficient quantity of data to generate the tool via a global optimization problem. The challenge is to have sufficiently rich and varied data to represent the problem in all its facets. This is often a stumbling block in AI projects, where accumulating and annotating data is extremely costly.

Here, the authors make a choice that we are seeing more and more in Deep Learningsince the famous work ofOpenAI work at Domain Randomization in which researchers trained a robotic agent on completely synthetic scenarios. This axis is increasingly used as a gas pedal, where we train a model on synthetic data and reserve real data for testing and quality control.

Here, this approach is fundamental, and we propose to detail how synthetic data is generated. Deepmind has generated 100 million examples of demonstrations using a very interesting approach:

• First, the authors generate a large number of geometric figures of varying complexity. These figures are the starting points for each demonstration.
• The authors then use the mathematical “symbolic” engines to create new, slightly more complex mathematical statements. The engine can use these statements as new starting points to build new ones.

If we stop here, we’ll have generated an example of a demonstration, but this example can easily be solved by the mathematical engine that built the tree of assertions. The originality here lies in the definition of geometric elements that need to be constructed to arrive at the proof, in other words: the authors will identify points in the generated problem that are important for arriving at the demonstration, but which may have been omitted in the initial definition of the problem. These points then become intermediate constructions to be carried out in order to arrive at the proof. And this is where we depart from the results that can be generated by a symbolic engine in mathematics! These engines are incapable of generating new geometric elements for use in a demonstration. The problem then becomes a more complex one, stored in the dataset synthetic. Based on the Deepmind :

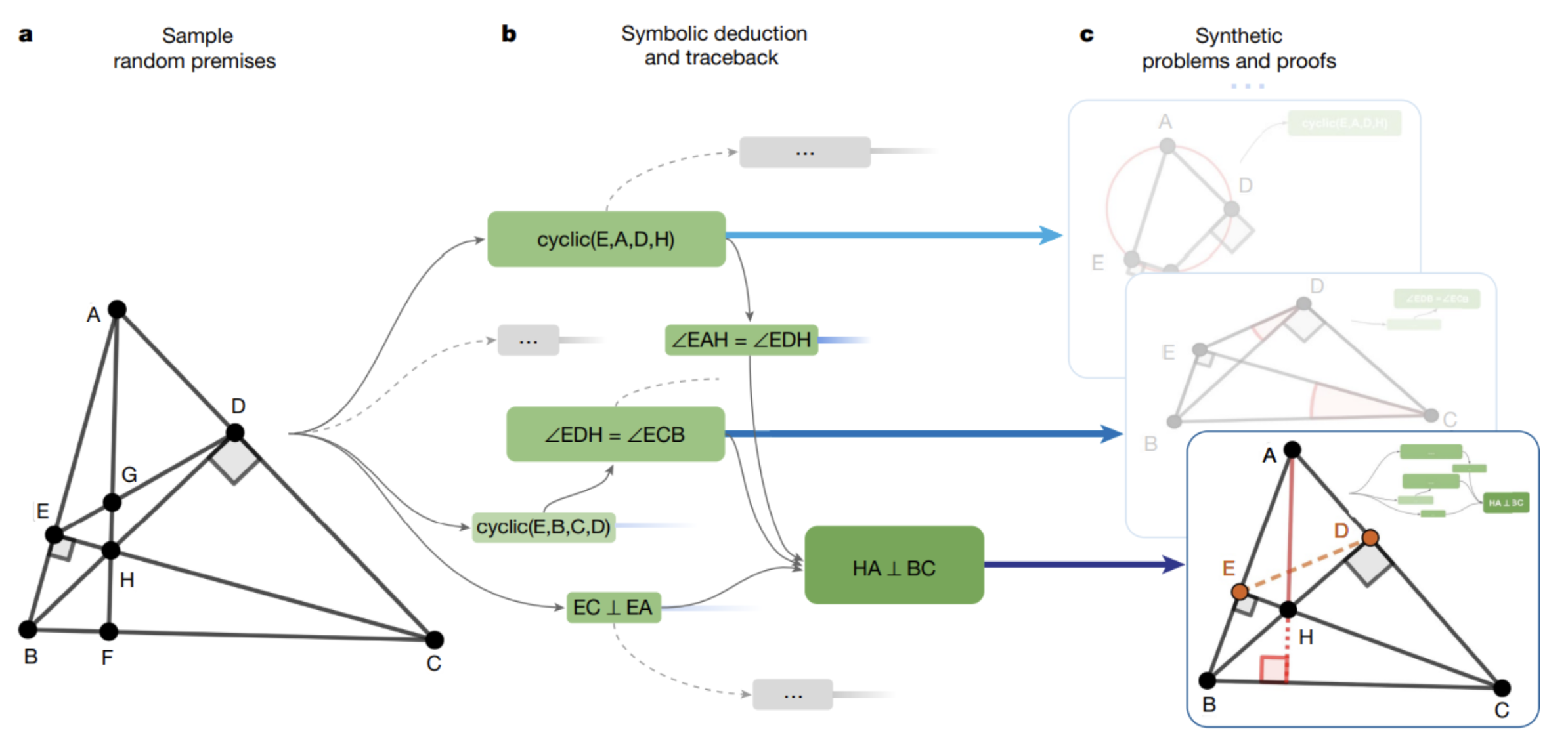
1. The authors start from an initial geometric scenario.
2. The symbolic engine builds up a certain number of assertions, until it retains a final assertion which will be the objective of the problem, above, the fact that (HA) is perpendicular to (BC). Following this choice, the authors have already deleted all the assertions generated that are not useful for the chosen solution (in the diagram, the assertions retained are in green).
3. Points E and D are not useful for defining the problem. They are therefore considered as intermediate constructs that the model will have to generate, and are therefore removed from the initial problem definition.

When generating synthetic data, one important point is to have a high degree of variance in the data. Put another way: we don’t want “just” lots of examples, we want to check that this set of examples acts as a valid representation of the overall problem to be addressed. Here, the authors have analyzed this dataset, and observed a very interesting variance: we find problems that are smaller than large (diagram below), but with very different cases, from “simplistic” problems (collinearity of points) to problems worthy of the Olympiads, via re-discovered theorems (case below of length 20).

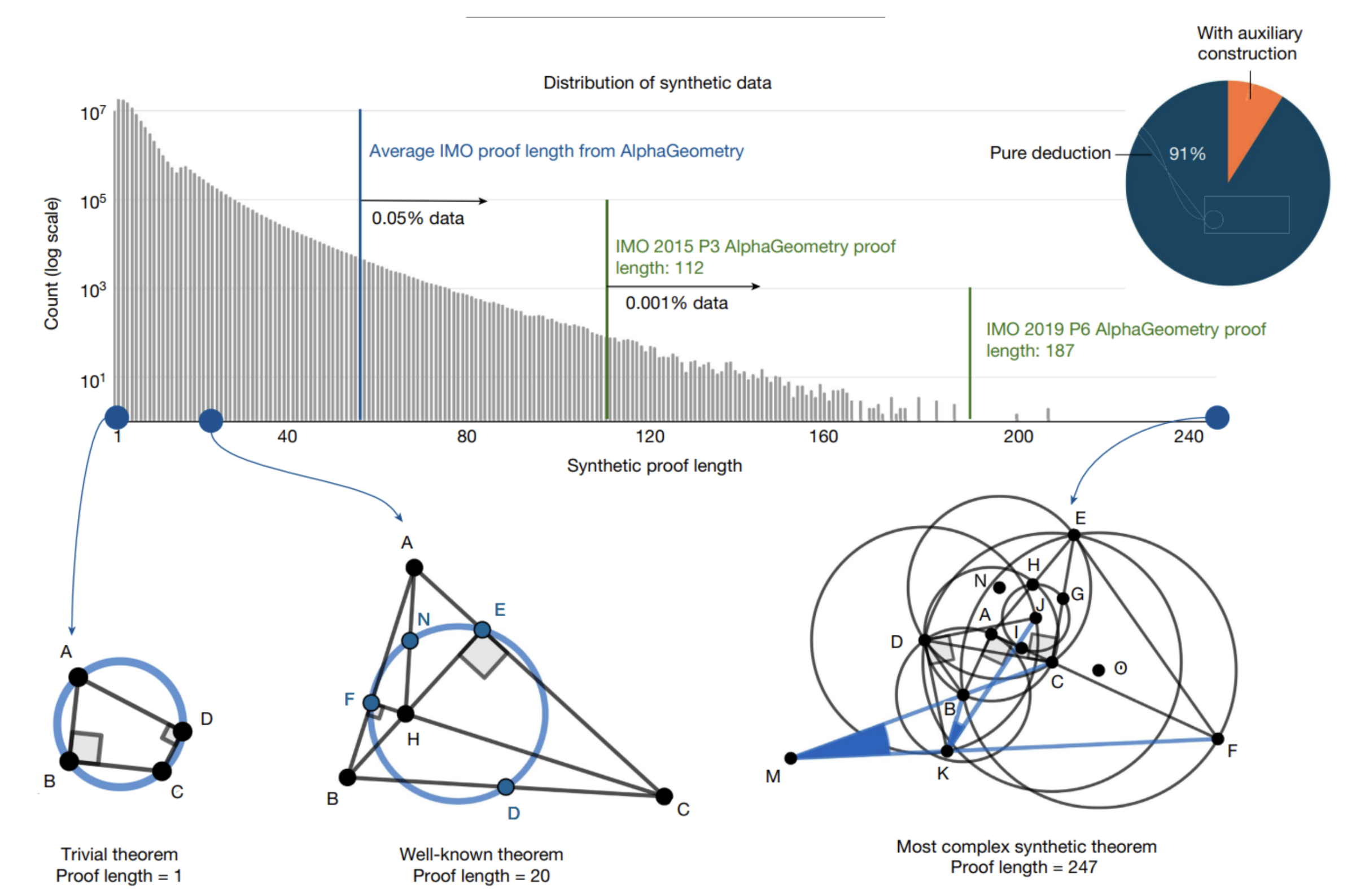
We note that only 9% of the problems generated use auxiliary constructions. This figure may seem low, but as we shall see, the presence of these problems is fundamental to the success of AlphaGeometry.

The alliance of LLM and the symbolic engine

To my right! An efficient symbolic engine, but very limited in its search capabilities, which has the advantage of being able to explore a tree of possibilities in an optimal way and confirm whether a solution is valid or not.

To my left! A Large Language Modeltrained to reproduce the distribution of a language, capable of breathtaking results, but also of prodigious failures, notably hallucinations in its predictions that can occur at any time and without warning.

Nobody’s going to win, and it’s the combination of these two approaches that generates a revolutionary tool for mathematical demonstration. This point is all the more interesting as it foreshadows a form of use for the Deep Learning which we have already seen, and which (in certain cases) enables us to avoid the pitfalls of artificial intelligence as we know it today.

Let’s start by detailing what Deepmindhas done, before moving up a bit to consider whether this type of combination can be adapted to other problems. 🙂

The Language Modelalready, is a model that’s not all that complex compared with the models we usually see (GPTs, Llamas, etc.), with around 100 million parameters. This model is going to be trained on a very particular language, modeling exactly the geometrical problems, to complete demonstrations. Like all models Deep LearningThis model is perfectly capable of hallucinating absurdities at any moment, but is a fundamental tool for exploring the universe of possibilities and proposing new solutions.

Two symbolic engines are used by AlphaGeometry. Based on a set of mathematical observations, these engines will search for a proof by applying mathematically valid combinations of these observations.

The fascinating thing is how these two tools work together. Indeed, the Language Model will only be used to generate intermediate constructions (new geometric elements) in the problem. Symbolic engines, on the other hand, will start from existing elements and constructions added by the LLM to see if they can reach the result by combination. If they fail, the LLM will be recalled with a prompt enriched by the latest experimentation. The diagram below illustrates this approach. In the scenario at the top of the diagram, the LLM has just generated the midpoint D of [BC]. Generally speaking, the contributions of the LLM are highlighted in blue below.

Let’s take a step back. The combination of these models is interesting here: at high level, we have :

• A generative Deep Learning model that will learn the distribution of the data and generate new, original elements, with unquestionable creative capacity. On the other hand, this model is capable of saying anything at any time (the hallucination drama that has been going on since 2012…).
• A system for testing and validating (or not) a generated element. This system serves as a compass for filtering (or even directing) the use of the model. Deep Learning.

This type of approach is not fundamentally new; we’ve already come across generative subjects that use it directly. The case of robotics with digital twins is typically not very far off, where we’ll have an agent trained via Deep Reinforcement Learning to generate new actions, but where these actions are validated against the digital twin before being stored and used.

This type of approach is likely to explode in combination with language models such as GPTs, Mistral or other LLamas. In fact, there is no single technique that can provide absolute and correct protection against hallucinations. Consequently, creating an algorithm that regularly interrogates one of these models, then confirms that the result is correct and, if the result poses a problem, re-interrogates the model, is a much more constructive and reliable approach than what exists in the majority of cases. In fact, we identified one such case in one of our research reviews, published in June 2023 ( https://datalchemy.net/ia-quel-risque-a-evaluer-les-risques/). Indeed, researchers had developed an agent playing Minecraft which performed this type of iteration, between language model suggestions and formal validation.

This alliance is perhaps one of the “hidden gems” of the publication, in that it presages a very generic approach to addressing new problems. We (Datalchemy) have already had the opportunity to implement this type of exchange (at a much more humble level, it must be said) with very interesting results. Having said that, we can already see that we’re far from implementing real-time processing, and are more interested in exploratory approaches. Conception/design of new objects or mechanisms in the face of a digital twin, optimization of physical or robotic problems are already obvious. Beyond that, we could be interested in the extension to a logical problem, perfectly illustrated here by geometry. The relevance of such an extension will be directly linked to our ability to correctly model a valid model via a system of rules. Geometry (and mathematics more generally) is the “simplest” case in point, in that a mathematical demonstration is not, by its very nature, confronted with a real experiment. The more random the target subject, or the more complex it is to model “perfectly”, the less interesting the approach will be. That said, we can imagine approaches that don’t automate the discovery of the solution, but rather accelerate it, by modeling only to filter out as best we can the predictions of a LLM and to keep only the most interesting samples for expert consultation.