AlphaGeometry: What lessons to draw from DeepMind's latest feat?

"Check out the magazine version by clicking here."

"If you only have a minute to read now, here's the essential content in 7 points:"

1. DeepMind has once again made a strong impact with a system capable of solving highly advanced geometric problems.
2. This system offers an interesting combination between a Large Language Model and a formal verification system (referred to here as “symbolic AI”).
3. The Large Language Model mainly contributes, in the construction of a proof, the ability to suggest the creation of new elements (such as the construction of a point or a line).
4. The formal validation systems aim to combine various observations to generate the final proof.
5. An essential element of success is the generation of millions of synthetic example demonstrations, without which the model would never have been able to function.
6. A key lesson is the combination of the LLM and the validation system, which can extend to many other scenarios.
7. The second important lesson, which we already knew, is the vital importance of synthetic data (noting that here, it can be "perfect"), without which this type of result could not even exist.

• 5 keywords

#Symbolic AI; #Large Language Models; #DeepMind; #Synthetic Data; #Solution Space Exploration

• Why reading this publication can be concretely useful to you?

Deepmind made quite a splash with this AI that can solve complex geometry problems. This approach offers us several theoretical and practical lessons to address other problems with Deep Learning: how to combat hallucinations, the value of synthetic data for addressing a problem, etc.

• What you can tell a colleague or your boss about it?

Datalchemy has thoroughly detailed Deepmind's latest feat in AI and geometry. Moreover, they have fun drawing lessons from it that we can apply to our internal AI problems. Already on synthetic data, but also on the use of an LLM despite its ability to tell anything. What's amusing is that the LLM is just a small part of the solution, but this small part is absolutely indispensable.

• Which business processes are likely to be modified based on this research?

Most creation processes faced with a simulator or digital twin will draw inspiration (or already are inspired) from this type of architecture. Furthermore, topics where the problem can be formally modeled are excellent candidates for adapting this work.

• The use cases we have developed for clients that relate to the topic of this research echo?

Optimization of a digital twin. Control and framing of a Large Language Model.

Here we go...

This month, we're focusing on a single, very recent publication that has had a resounding impact in the field of artificial intelligence: AlphaGeometry. This recent work by DeepMind has enabled the creation of an agent capable of solving numerous geometric problems from an international competition.

We propose to detail the approach taken by DeepMind, firstly to dispel a number of fantasies or misconceptions that have proliferated on the Internet following this work. For example, we have heard a lot about symbolic AI, which, while it exists, remains a subject to clarify. Furthermore, we will extract the most important elements of the DeepMind approach to see if this type of approach can be generalized to other subjects. We will see that two points of AlphaGeometry can be generalized and allow us to envisage a new form of AI approach that enables working using the best of neural networks, but abstracting away from their biggest flaws, notably hallucinations.

[https://www.nature.com/articles/s41586-023-06747-5]

AlphaGeometry – Detailed Analysis of an AI Solving Geometry Problems.

What happened?

Let's start by summarizing this work and the objectives it has achieved. While we are typically among the more critical actors when it comes to new AI research, we must acknowledge that Deepmind has achieved some quite incredible and particularly interesting results here.

The fundamental idea is to address the resolution of a Euclidean geometric problem. The AI model (we're staying at a high level for now) will receive the basics of a problem, such as the presence of a certain number of geometric elements (points, lines, etc.) and rules about these elements (collinear points, angle values, etc.). The AI model also has an objective, a mathematical statement that must be rigorously demonstrated from the initial elements. Below is an example of a problem submitted to the model :

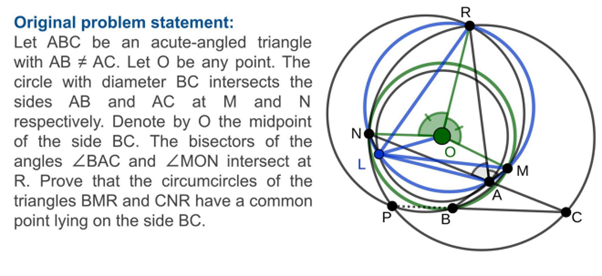
Designing a model capable of solving this type of problem is interesting in itself. Mathematics is a global field that underlies a large number of more generic logical problems, and geometry is one of the more specific domains of mathematics: it has, on one hand, an appreciable "simplicity" of definition (the number of operations that can be performed remains limited compared to what can be found in other scientific domains). But at the same time, the proofs to be generated can become extremely complex, posing a real challenge for the model.

Here, the cannon shot came from the model's results, which were able to solve almost all of the problems from the IMO, International Mathematics Olympiad, a highly prestigious international competition.

Another element widely shared on social networks is the use of "symbolic AI". The quotation marks are essential here because while the term is accurate, it has been the source of many fantasies about Deepmind's work. Can artificial intelligence manipulate symbolic concepts like a human? The answer here is no. And it's time to delve into this topic a bit more precisely 🙂

Symbolic AI?

The term "artificial intelligence" is an extremely dangerous term. This term evokes a ton of quite classic fantasies from science fiction, and while it was used by researchers in Deep Learning as far back as the 1980s, it is now a source of confusion. When we talk about Language Models, agents playing Go, Generative AI, we are actually talking about the field of Deep Learning, which involves training massive models on a quantity of data that represents the problem to be solved. Beyond a simple battle over words, we have observed many times that it is important to seek out the right definitions in order to limit misunderstandings which often harm an AI project.

But then, what is Symbolic AI? Behind this term lies a vast catch-all encompassing many algorithmic approaches that were heavily utilized from the 1950s to the 1990s. Symbolic AI refers to a system of rules where solutions can be constructed through logical combinations of these rules. Expert systems, predecessors of Deep Learning, are a part of this. In the context of AlphaGeometry, we refer to Symbolic AI because mathematical inference engines are used. These engines store a set of rules to construct, from statements about a problem, new, more complex statements. These engines create a graph by combining stored and generated statements, hoping that the model eventually finds the proof we seek.

In AlphaGeometry, two mathematical inference models are employed by Deepmind. It's important to emphasize that these models aren't anything new compared to what existed before. These engines are complemented by a neural network, a Large Language Model. It's the combination of these two tools that has allowed Deepmind to achieve convincing results, and this combination will be particularly interesting to us, as it has already been extended to other problems and offers an intriguing solution to some drawbacks of Deep Learning.

That said, the term 'symbolic AI' must be handled with particularly fine tweezers here. We don't have a new form of AI tools capable of manipulating high-level symbols. We have relatively old tools that use a system of rules and concepts to deepen understanding. We'll explore further the limitations and conditions for applying this principle to other problems.

Generation of synthetic data

A fundamental point for Deepmind's results, and unfortunately often overlooked (probably because it's a bit less sexy than the term "symbolic"). However, this point is, on one hand, an element without which nothing would have been possible, and on the other hand, it represents a relevant lesson about artificial intelligence in general.

Indeed, let's go back to basics. The revolution of artificial intelligence, which began in 2012, is based on Machine Learning, which presents a new paradigm. In Machine Learning, we no longer write the exact algorithm that will determine the solution; instead, we prefer to represent the problem with a dataset, which is a sufficient amount of data, and then generate the tool through a global optimization problem. The challenge is to have data that is rich and varied enough to represent the problem in all its facets. This point is often a stumbling block in an AI project, where accumulating and annotating data is extremely costly.

Here, the authors make a choice that we increasingly observe in Deep Learning, since the famous work of OpenAI on Domain Randomization in which researchers trained a robotic agent on entirely synthetic scenarios. This approach is becoming more and more common, where a model is trained on synthetic data, and real data is reserved for testing and quality control.

Here, this approach is fundamental, and we propose to detail the mode of generation of synthetic data. Deepmind has indeed generated 100 million demonstration examples through a very interesting approach :

• Firstly, the authors generate a large number of geometric figures, more or less complex. These figures are the starting points of each demonstration.
• The authors then use mathematical "symbolic" engines to create new mathematical statements, a bit more complex. The engine can use these statements as new starting points to build new ones.

If we stop here, we will have generated a demonstration example, but this example can easily be solved by the mathematical engine that constructed the tree of statements. The originality here is to define geometric elements that need to be constructed to arrive at the proof, in other words: the authors will identify points in the generated problem that are important for reaching the demonstration but that may be omitted in the initial definition of the problem. These points then become intermediate constructions to be made to arrive at the proof. And that's where we move away from the results that a symbolic engine can generate in mathematics! These engines are indeed unable to generate new geometric elements to then use them in a proof. The problem then becomes a more complex one that will be stored in the synthetic dataset . Referring back to the Deepmind :

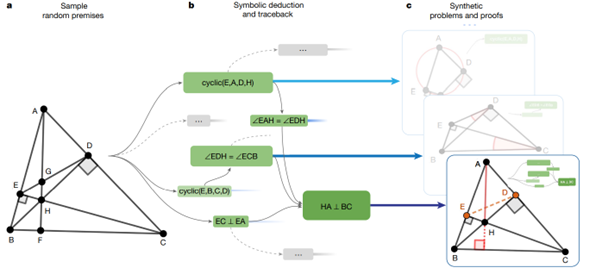
1. The authors start with an initial geometric scenario.
2. The symbolic engine constructs a certain number of statements, until it retains a final statement that will be the objective of the problem, above, the fact that (HA) is perpendicular to (BC). Following this choice, the authors already remove all the generated statements that are not useful for the selected solution (in the diagram, the retained statements are in green)
3. Points E and D are not useful for defining the problem. They are therefore considered as intermediate constructions that the model will have to generate, and are thus removed from the initial definition of the problem.

When generating synthetic data, an important point is to have significant variance in the data. In other words, we don't just want "a lot" of examples; we want to ensure that this set of examples serves as a valid representation of the overall problem to be addressed. Here, the authors analyzed this dataset and observed a very interesting variance: there are smaller problems as well as larger ones (as shown in the diagram below), but with very different cases ranging from "simplistic" problems (collinearity of points) to problems worthy of Olympiads, including rediscovered theorems (as in the case below with a length of 20).

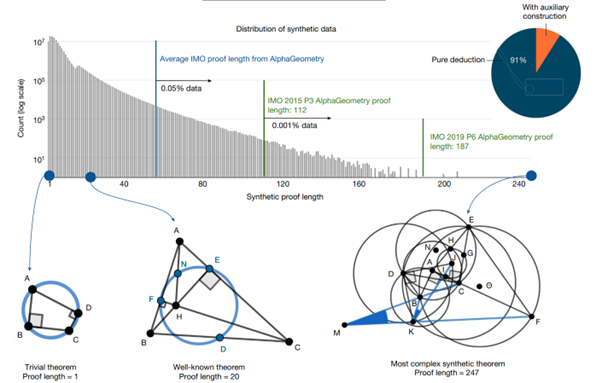
We note that only 9% of the generated problems use auxiliary constructions. This figure may seem low, but the presence of these problems, as we will see, is fundamental to the success of AlphaGeometry.

The alliance of the LLM and the symbolic engine

To my right! An efficient but very limited symbolic engine in its search capabilities, which has the advantage of being able to explore a tree of possibilities optimally and confirm whether a solution is valid or not.

To my left! A Large Language Model, trained to reproduce the distribution of a language, capable of astonishing results, but also of prodigious failures, especially hallucinations in its predictions that can occur at any time and without warning.

No one approach will win, and it's the combination of these two approaches that allows for the creation of a revolutionary mathematical demonstration tool. This point is all the more interesting as it foreshadows a form of Deep Learning utilization that we have already observed and that allows us to overcome (in some cases) the pitfalls of artificial intelligence as we know it today.

Let's start by detailing what Deepmind has done before stepping back a bit to reflect on the ability to adapt this type of combination to other problems 🙂

The Language Model, for starters, isn't as complex as the models we typically see (like GPTs, Llamas, etc.), with around 100 million parameters. This model will be trained on a very specific language, precisely modeling geometric problems, to complete demonstrations. Like any Deep Learning model, this one is perfectly capable of hallucinating absurdities at any moment, but it's a fundamental tool for exploring the realm of possibilities and proposing new solutions.

Two symbolic engines are employed by AlphaGeometry. These engines will allow, based on a set of mathematical observations, to search for a proof by applying combinations of these observations that are mathematically valid.

The fascinating point is how these two tools are combined. Indeed, the Language Model will be used solely to generate intermediate constructions (new geometric elements) in the problem. The symbolic engines, on the other hand, will start from the existing elements and the constructions added by the LLM to try to see if they can reach the result by combination. In case of failure, the LLM will be recalled with a prompt enriched by the latest experiment. The diagram below represents the approach. In the scenario depicted at the top of the diagram, the LLM has only generated the point D, the midpoint of [BC]. In general, the contributions of the LLM are highlighted in blue below.

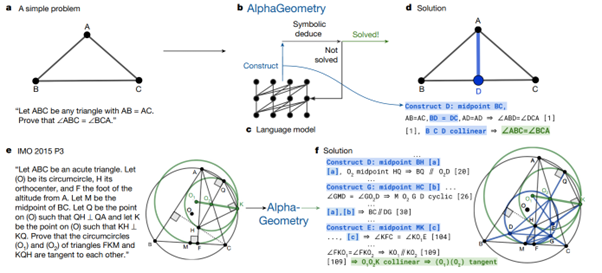
Let's take a step back. The combination of these models is interesting here, we have, at a high level :

• A generative Deep Learning model that learns the data distribution and generates new original elements, with an undeniable capacity for creation. However, this model is capable of saying anything at any time (the drama of hallucinations that has been going on since 2012...)
• A system that allows testing and validating (or not) a generated element. This system serves as a compass to filter (or even guide) the use of the Deep Learning model.

This type of approach is not fundamentally new; we have already encountered generation tasks that use it directly. The case of robotics with digital twins is typically not very different, where we train an agent via Deep Reinforcement Learning to generate new actions, but where these actions are validated against the digital twin before being retained and used.

This type of approach is likely to explode in combination with language models like GPTs, Mistral, or other LLamas. Indeed, no technique provides complete and absolute protection against hallucinations. Therefore, creating an algorithm that regularly queries one of these models and then confirms that the result is correct, and if the result is problematic, re-queries the model, is a much more constructive and reliable approach than what exists in the majority of cases. In fact, we had identified one such case in one of our research reviews, published in June 2023 (https://datalchemy.net/ia-quel-risque-a-evaluer-les-risques/). Indeed, researchers had developed an agent playing Minecraft that operated this type of iteration, between suggestions from a language model and formal validation.

This alliance may be one of the "hidden gems" of the publication, in that it foreshadows a very generic approach to addressing new problems. We (Datalchemy) have already had the opportunity to implement this type of exchange (at a much more humble level, it must be said) to achieve very interesting results. However, we already see that we are far from real-time processing implementations, more on exploration approaches. Designing new objects or mechanisms facing a digital twin, optimizing physical problems, robotics are already obvious applications. Beyond that, we can consider extending to a logical problem, as illustrated perfectly by geometry here. The relevance of such an extension will be directly related to our ability to model a valid system of rules. Geometry (and mathematics more generally) is the "simplest" case study, in that a mathematical proof is, by nature, not confronted with real-world experience. The more random the target subject, connected to human operators, or complex to model "perfectly," the less interesting the approach will be. However, we can imagine approaches that not only automate the discovery of the solution but also accelerate it by modeling only to filter the predictions of an LLM as effectively as possible and keep only the most interesting samples for expert consultation.